Rotational kinetic Energy: Derivation, Formula, Examples, Unit

Introduction:

Rotational kinetic energy, as the name shows, occurs due to the rotation of an object. We can observe that linear velocity is different at every point on a rotating cycle of the body about its axis. Rotational kinetic energy arises due to the spinning or rotating motion of a mechanical component such as a flywheel or rotating shaft, whirring of a spinning top, or rotation of a wind turbine.

In this article, we will discuss its formulas, derivations, units, and examples.

Definition of Rotational Kinetic Energy

Rotational kinetic energy is expressed as the rotation of an object on its axis. Similar to linear kinetic energy which is expressed as the motion of an object, rotational kinetic energy means the spinning of an object around its axis. Rotational kinetic energy is also discussed as a function of the angular velocity and the moment of inertia which relate it to the total kinetic energy.

Formula of Rotational Kinetic Energy

Through the formula, we can easily understand the rotational kinetic energy. Its equation is:

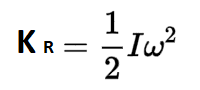
Where:

• K_R​ shows the Rotational Kinetic energy
• I is the moment of inertia (a measure of an object’s resistance to rotation)
• ω is the angular velocity (the measure of an object’s fast rotation)

Unit of Rotational Kinetic Energy

The unit of rotational kinetic energy in SI and MKS systems is as under:

SI Unit

Common units include joules (J), which are derived from the units of the moment of inertia (kg∙m²) and angular velocity (rad/s).

MKS Unit

Kilogram-Meter Squared per Second Squared (kg∙m²/s²)

Examples:

You can witness the examples and manifestations of rotational kinetic energy everywhere. For instance, the rotation of the earth as it is rotating around its axis, the rolling of wheels of a cycle or a car, etc.  The blades of a rotating fan also have rotational kinetic energy; the faster the blades move the higher their rotational kinetic energy.

Moment of Inertia and Rotational Kinetic Energy

The property of a rotating object that tells us the resistance to changes in velocity is known as the moment of inertia. There is a bond between the moment of inertia and rotational kinetic energy. The moment of inertia of point particles moving around a fixed axis, the more immense an object is the more inertia it has and the greater its resistance to change in linear velocity. Those objects which have larger moments of inertia require more energy to get the same angular velocity as compared to objects which are small having smaller moments of inertia.

Moment of inertia (I) is calculated differently for different shapes and masses. For a point mass (m) rotating at a distance (r) from the axis of rotation, the moment of inertia is given by

I=m*r²

The formula of the moment of inertia depends upon the shapes of the object like disks, rods, etc. When a larger moment of inertia implies resistance is greater to changes in rotation. For instance, figure skater tucks their limbs into wheel spinning to decrease their moment of inertia and spin faster. On the other hand, a diver extends their body to increase the moment of inertia and control their rotational speed.

Rotational Kinetic Energy Derivation

From the analogy between transitional velocity (v) and angular velocity (ω), and between linear momentum (p) and angular momentum (L), the formula for rotational kinetic energy can be derived.

The derivation of rotational kinetic energy tells us the connection between an object’s spinning motion and its energy. A few steps are as under to  elaborate the derivation of rotational kinetic energy:

Step 1

Consider an object with mass(m) moving around a fixed axis with angular velocity(ω).

Step 2

The energy of a mass element dm at a distance r from the axis is

dKE_rot​ = 0.5 * dm * r² * ω²

Step 3

By combining the energy contributions from all dm, we have

K_Erot =∫ 0.5 * r² * ω² *dm

Step 4

The rotational resistance of an object is reflected in the moment of inertia (I). That is

I =∫ r² * f(r) * dr

Step 5

You can substitute I into the integral and get the following formula

K_Erot =1/2 * I * ω²

Rotational Kinetic Energy Problems and Solutions

A wheel with a moment of inertia I=0.5kg⋅m2 is rotating at an angular velocity ω=4rad/s. Calculate its rotational kinetic energy.

Solution: The formula for rotational kinetic energy is given as:

K_Erot =1/2 * I * ω²

Use the given values in the formula:

K_Erot = 1/2 x (0.5  kg⋅m² ) x ( 4 rad/s ) ²

K_Erot = 0.5 x 0.5kg⋅m² x 16 rad²/s²

After calculation, we get;

K_Erot = 4 Joules

Conclusion

To conclude this article, Rotational kinetic Energy is a force bringing rotation to life from the spins and twirls which change our world. It shows that energy is not present in linear motion, but also in the intriguing arena of rotation.

FAQ’s